Сегодня мы рассмотрим как найти площадь поверхности правильной призмы с примерами и формулами.
Одним из важных многогранников, свойства которого подробно изучают в стереометрии, является призма. В статье рассмотрим эту фигуру, раскрывая подробнее вопрос, что это - правильная призма. Также приведем формулы, позволяющие вычислить ее объем и площадь.
Фигура призма
Призма - это геометрическая фигура, которая состоит из n + 2 граней, где n - количество сторон плоского многоугольника. Две грани призмы являются абсолютно одинаковыми многоугольниками. Они расположены в параллельных плоскостях и называются основаниями. Стороны оснований соединяются между собой параллелограммами. Этих параллелограммов n штук, все они образуют боковую поверхность пространственной фигуры.
Помимо граней, призма имеет вершины (2 × n) и ребра (3 × n). Вершины все являются однотипными, а вот ребра бывают двух видов: относящиеся к основаниям и к боковым сторонам.
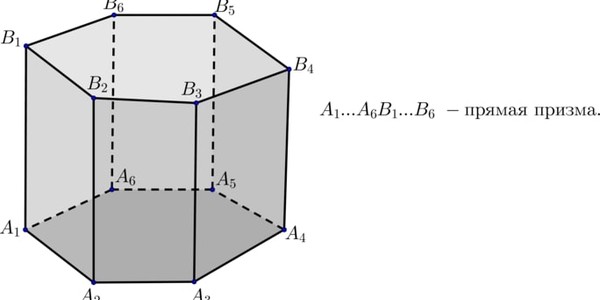
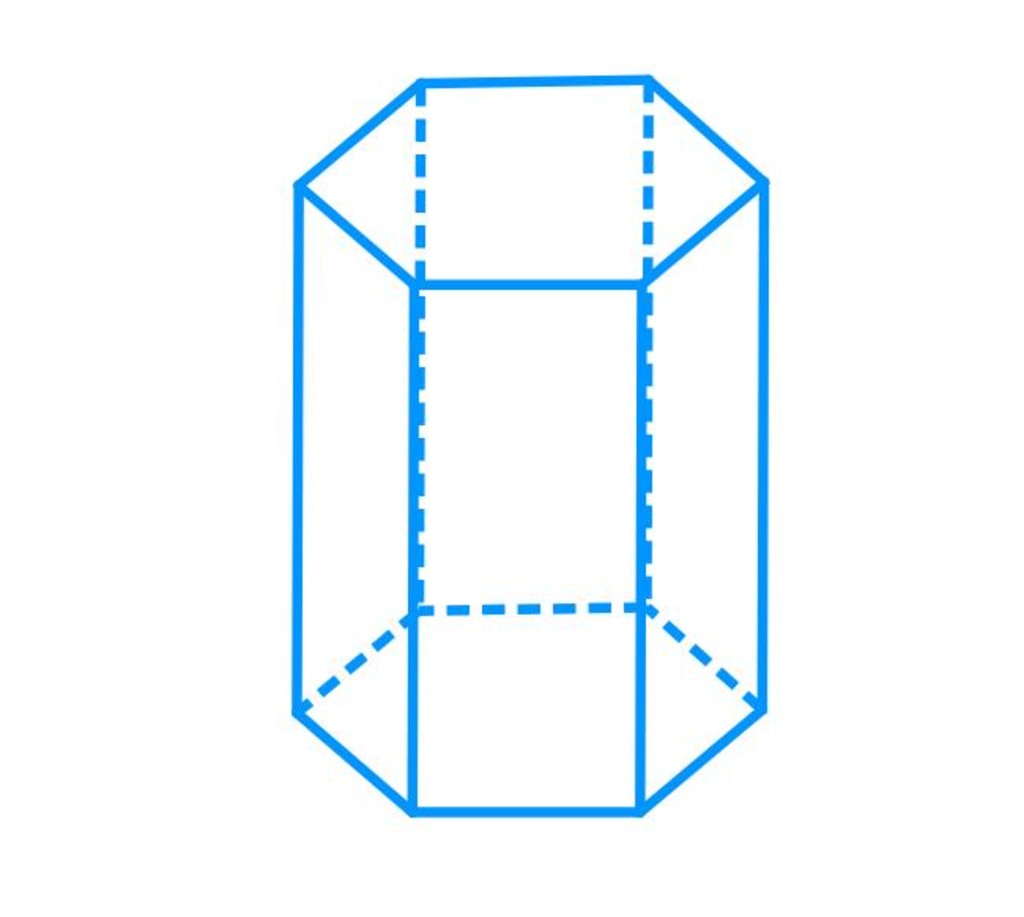
Любую призму можно получить, если параллельно самому себе перенести многоугольник из одной плоскости в другую в пространстве. Ниже показан пример шестиугольной призмы, имеющей два шестиугольных правильных основания. Как можно видеть из рисунка, ее боковая поверхность образована шестью прямоугольниками (частный случай параллелограммов). Такая фигура является правильной призмой. Рассмотрим подробнее ее в статье.
Что это - правильная призма?
Существует несколько разных классификаций призм. Так, бывают фигуры прямые или наклонные, выпуклые и вогнутые, пятиугольные и десятиугольные, но самая симметричная среди всех изучаемых фигур - это правильная призма. Под ней полагают такую фигуру, которая имеет правильное основание и является прямой. Разберем по порядку каждый пункт этого определения.
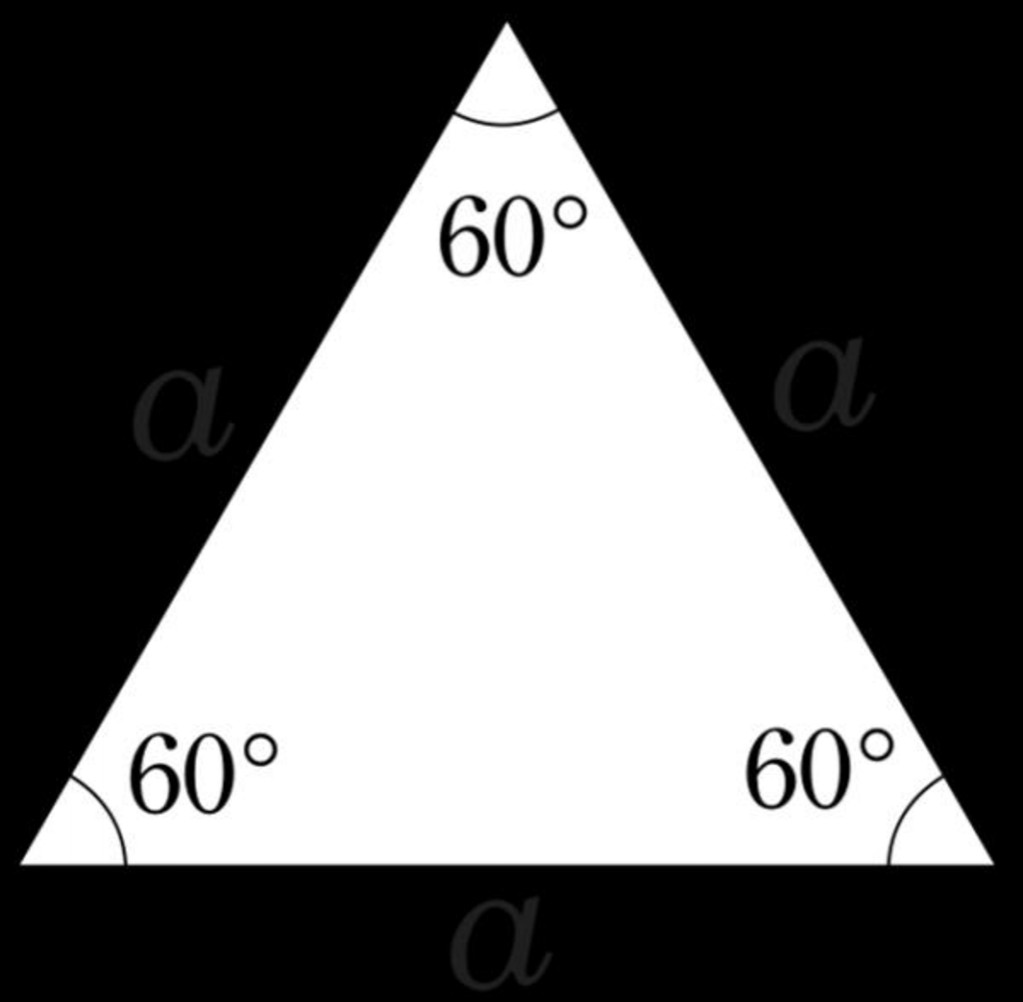
Под правильным основанием призмы понимают многоугольник, который имеет все одинаковые стороны и все одинаковые углы. Самым простым из таких многоугольников является треугольник равносторонний, углы которого равны 60o. Далее, увеличивая количество сторон, получаем квадрат, правильные пятиугольник и шестиугольник и так далее.
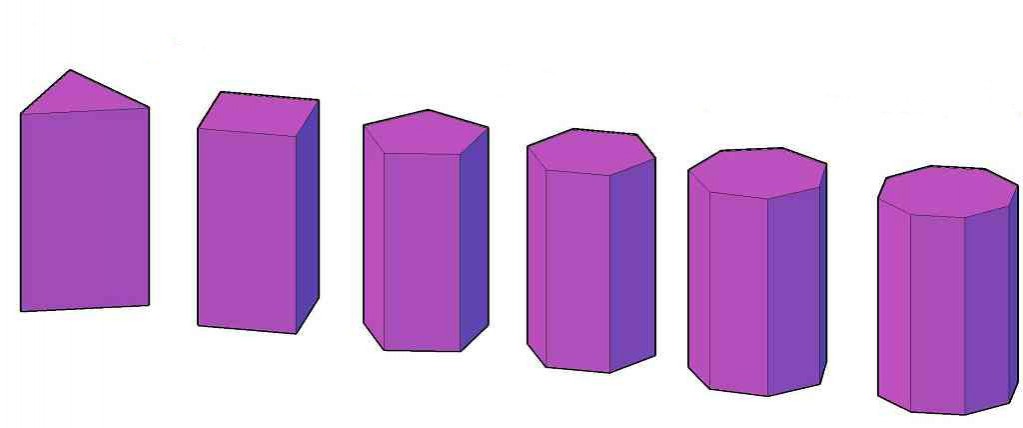
Как было сказано в определении, правильная призма - прямая призма. Призмой прямой называется такая фигура, у которой все боковые параллелограммы представляют собой прямоугольники. Более того, эти прямоугольники перпендикулярны основаниям. Последний факт приводит к тому, что длина бокового ребра любого из прямоугольников оказывается равной высоте фигуры. На рисунке ниже показан набор призм правильных (начиная от треугольной и заканчивая восьмиугольной).
Линейные параметры фигуры
Разобравшись, что это - правильная призма, дадим характеристику параметрам, которые используются для ее описания. В первую очередь это длина стороны ее основания a и высота h. Как было отмечено, высота равна длине бокового ребра b.
Помимо этих величин, также призмы характеризуются диагоналями. Диагонали бывают трех типов: лежащие в основаниях, на боковых сторонах и внутри самой фигуры. Расчет длин диагоналей предполагает использование теоремы Пифагора. Например, для правильной четырехугольной призмы объемные диагонали равны:
d1 = √(2 × a2 + b2).
Диагонали же основания d2 и боковых прямоугольников d3 составляют:
d2 = a × √2;
d3 = √(a2 + b2).
Заметим, что формула для диагоналей d3 будет одинаковой для любых многоугольных правильных призм. Что касается вычисления диагоналей d1 и d2 для других призм (пятиугольной, шестиугольной и так далее), то для этого следует проводить последовательные геометрические расчеты с учетом свойств соответствующих правильных многоугольников.
Вычисление площади и объема
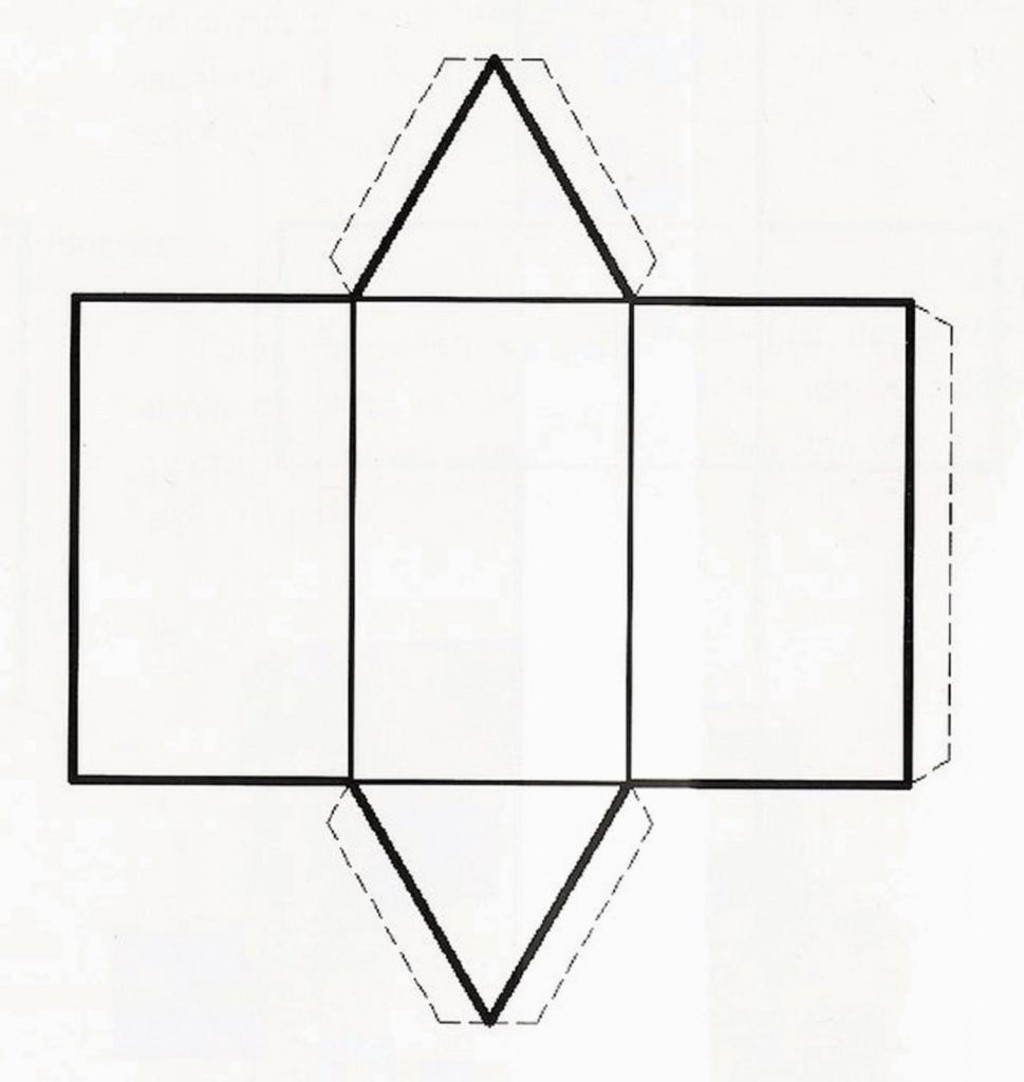
Площадь поверхности изучаемой фигуры представляет собой сумму площадей двух n-угольников и n прямоугольников. Площадь одного n-угольного основания можно рассчитать по следующей формуле:
Sn = n / 4 × ctg (pi / n) × a2.
Если обозначить буквой b боковое ребро, правильной призмы площадь боковой поверхности составит:
Sb = n × a × b.
Тогда суммарная площадь будет равна:
S = n / 2 × ctg (pi / n) × a2 + n × a × b.
Первое слагаемое в выражении - это площадь сразу двух оснований.
Объем призмы произвольного вида вычисляется так:
V = So × h
То есть достаточно умножить высоту h на основания площадь So, чтобы вычислить искомую величину. Поскольку мы знаем как рассчитывать площадь основания, то, подставляя соответствующую формулу в выражение для V, приходим к следующему результату:
V = n / 4 × ctg (pi / n) × × a2 × h.
Отметим, что для вычисления площади и объема изучаемого вида призм достаточно знать лишь два их линейных параметра.
Задача с призмой треугольной
Известно, что высота основания правильной треугольной призмы равна высоте объемной фигуры и составляет 11 см. Необходимо найти для этой призмы объем и площадь полной поверхности.
Из условия задачи нам известны два параметра, поэтому любые свойства фигуры можно однозначно рассчитать. Чтобы найти длину стороны треугольного основания, следует вспомнить свойства равностороннего треугольника. В частности, его высота одновременно является также биссектрисой. Это позволяет воспользоваться определением функции косинуса, чтобы длину высоты основания ha записать в следующем виде:
ha = a × cos(30o) = √3 / 2 × a.
Откуда вычисляем a:
a = 2 × ha / √3 = 12,7 см.
Поскольку a и h известны, то можно воспользоваться формулами для площади и объема:
S = n / 2 × ctg (pi / n) × a2 + n × a × b = √3 / 2 × 12,72 + 3 × 12,7 × 11 = 558,78 см2;
V = n / 4 × ctg (pi / n) × a2 × h = √3/4 × 12,72 × 11 = 768,25 см3.
При использовании формулы S мы применили свойство равенства высоты и ребра бокового для правильной призмы.
Выводы
Чтобы найти площадь поверхности правильной призмы необходимо пользоваться формулами и примерами представленными в данной статье.
Источники: fb.ru